In the course of my work I have to evaluate various Feynman integrals analytically. I use the framework of variation of mixed Hodge structures and the Feynman integrals arise as relative periods. They show interesting connections with mirror symmetry, number theory and the theory of D-modules, which can be used for concrete (analytical or numerical) evaluations of the Feynman integrals appearing in particle physics or gravity.

Graphs

Here is a list of the ones for which I have given an analytic expression. I refer to the Loopedia database that collects the various evaluations and links to the research papers

• Two-loop sunset Loopedia entry e111|e|:zzzz|z|
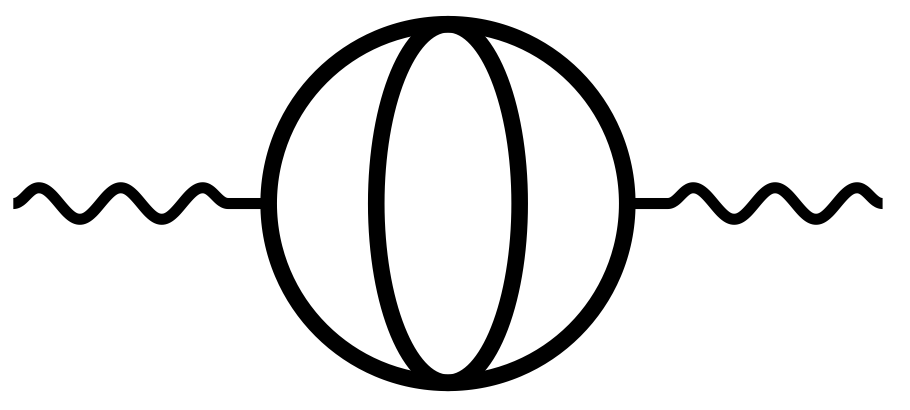
• Three-loop sunset all equal mass case : Loopedia entry e1111|e|:z1111|z|
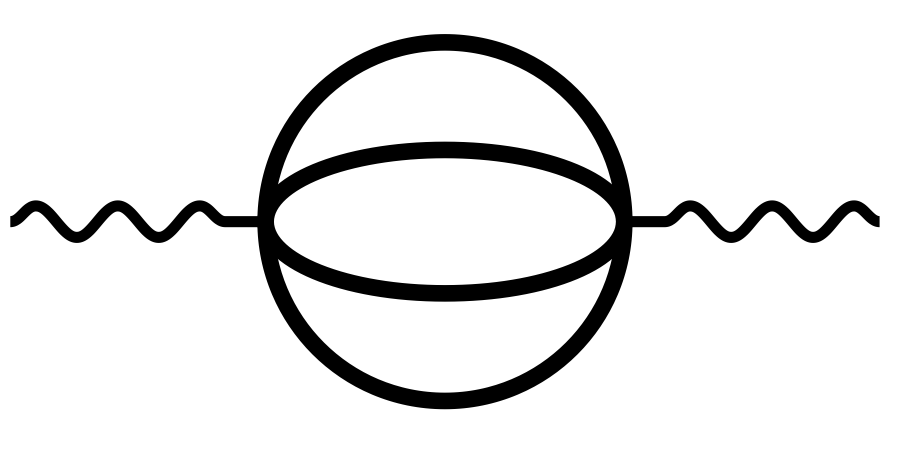
• The fat cat all equal mass case : Loopedia entry e1112|2|e|:z1111|1|z|
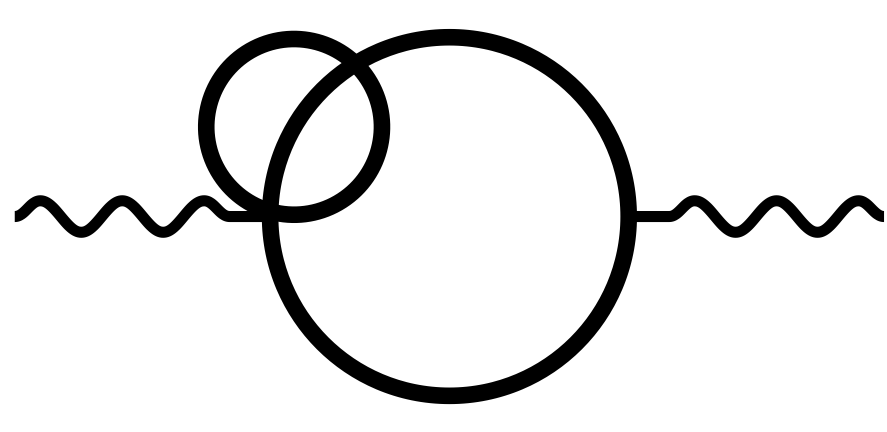
• The cat’s eye all equal mass case : Loopedia entry e12|223|3|e|:z11|111|1|z|

Methods

The methods I use are based on algebraic geometry seeing the Feynman integrals as relative periods of mixed Hodge structures

Motivic Period integrals

• The elliptic dilogarithm for the sunset graph published J.Number Theor. 148 (2015) 328
• A Feynman integral via higher normal functions published in Compos.Math. 151 (2015) 2329
• Local mirror symmetry and the sunset Feynman integral published in Adv.Theor.Math.Phys. 21 (2017) 1373

Hodge structure

• Motivic geometry of two-loop Feynman integrals published in Quart.J.Math.Oxford Ser. 75 (2024) 901

Picard-Fuchs equations

• Algorithms for minimal Picard-Fuchs operators of Feynman integrals published in Lett.Math.Phys. 113 (2023) 37
• Effective homology and periods of complex projective hypersurfaces published in Math.Comput. 93 (2024) 2985

Lectures notes

Here are some lecture notes explaining the approach

• Differential equations and Motives of Feynman integrals notes for the lectures given at the ICTP School on Number Theory and Physics 17 Jun 2024 – 21 Jun 2024
• Feynman integrals, toric geometry and mirror symmetry published in Elliptic Integrals, Elliptic Functions and Modular Forms in Quantum Field Theory
• Picard-Fuchs Equations of Twisted Differential forms associated to Feynman Integrals proceeding contribution of the conference Regulators V, 3-13 juin 2024 Department of Mathematics, University of Pisa, Italy
• Differential Equations for Feynman Integrals published as ISSAC ‘21: Proceedings of the 2021 on International Symposium on Symbolic and Algebraic Computation
• The physics and the mixed Hodge structure of Feynman integrals published as Proc.Symp.Pure Math. 88 (2014) 161

Reviews

General audience articles by me and others on the above results

• Putting a period on mathematical physics an article by Ursula Whitcher for the AMS Mathematical Reviews with an account of my calculation of the sunset Feynman integral with Spencer Bloch

• Des algorithmes efficaces calculent les amplitudes de diffusion english version